Note
Go to the end to download the full example code.
EarthDaily Simulated Dataset
Following a pivot field
Import librairies
import datetime
import earthdaily
from dask.diagnostics import ProgressBar
from matplotlib import pyplot as plt
from earthdaily import datasets, EarthDataStore
ProgressBar().register() # to have chunks progress bar
Loading pivot
pivot = datasets.load_pivot_corumba()
Init earthdatastore with environment variables or default credentials
eds = EarthDataStore()
Define timerange
delta_days = 10
datetime_list = ["2018-10-01", "2019-04-15"]
Request items for vnir dataset
items = eds.search(
"earthdaily-simulated-cloudless-l2a-cog-edagro",
intersects=pivot,
datetime=datetime_list,
query={"instruments": {"contains": "vnir"}},
prefer_alternate="download",
)[::delta_days] # an keep on item every n delta_days
Generate datacube for RGB and NIR
datacube = earthdaily.earthdatastore.datacube(
items, intersects=pivot, assets=["blue", "green", "red", "nir"]
).load()
[ ] | 0% Completed | 153.60 us
[ ] | 0% Completed | 100.36 ms
[ ] | 0% Completed | 200.53 ms
[ ] | 0% Completed | 300.68 ms
[ ] | 0% Completed | 400.87 ms
[ ] | 0% Completed | 501.08 ms
[ ] | 0% Completed | 601.24 ms
[ ] | 0% Completed | 701.48 ms
[ ] | 0% Completed | 801.68 ms
[ ] | 0% Completed | 901.87 ms
[ ] | 0% Completed | 1.00 s
[ ] | 0% Completed | 1.10 s
[ ] | 0% Completed | 1.20 s
[ ] | 0% Completed | 1.30 s
[ ] | 0% Completed | 1.40 s
[ ] | 0% Completed | 1.50 s
[ ] | 0% Completed | 1.60 s
[ ] | 0% Completed | 1.70 s
[ ] | 0% Completed | 1.80 s
[ ] | 0% Completed | 1.90 s
[ ] | 0% Completed | 2.00 s
[ ] | 0% Completed | 2.10 s
[ ] | 0% Completed | 2.20 s
[ ] | 0% Completed | 2.30 s
[ ] | 0% Completed | 2.40 s
[ ] | 0% Completed | 2.50 s
[ ] | 0% Completed | 2.60 s
[ ] | 0% Completed | 2.70 s
[ ] | 0% Completed | 2.81 s
[ ] | 0% Completed | 2.91 s
[ ] | 0% Completed | 3.01 s
[ ] | 1% Completed | 3.11 s
[ ] | 1% Completed | 3.21 s
[ ] | 1% Completed | 3.31 s
[ ] | 1% Completed | 3.41 s
[# ] | 2% Completed | 3.51 s
[# ] | 3% Completed | 3.61 s
[# ] | 3% Completed | 3.71 s
[# ] | 3% Completed | 3.81 s
[## ] | 5% Completed | 3.91 s
[## ] | 5% Completed | 4.01 s
[## ] | 5% Completed | 4.11 s
[## ] | 5% Completed | 4.21 s
[## ] | 5% Completed | 4.31 s
[## ] | 5% Completed | 4.41 s
[## ] | 5% Completed | 4.51 s
[## ] | 5% Completed | 4.61 s
[## ] | 5% Completed | 4.71 s
[## ] | 5% Completed | 4.81 s
[## ] | 5% Completed | 4.91 s
[## ] | 5% Completed | 5.01 s
[## ] | 5% Completed | 5.11 s
[## ] | 5% Completed | 5.21 s
[## ] | 5% Completed | 5.31 s
[## ] | 5% Completed | 5.41 s
[## ] | 5% Completed | 5.51 s
[## ] | 5% Completed | 5.61 s
[## ] | 5% Completed | 5.71 s
[## ] | 5% Completed | 5.81 s
[## ] | 5% Completed | 5.91 s
[## ] | 5% Completed | 6.01 s
[## ] | 5% Completed | 6.11 s
[## ] | 5% Completed | 6.21 s
[## ] | 5% Completed | 6.31 s
[## ] | 5% Completed | 6.41 s
[## ] | 5% Completed | 6.51 s
[## ] | 5% Completed | 6.61 s
[## ] | 5% Completed | 6.71 s
[## ] | 6% Completed | 6.81 s
[## ] | 6% Completed | 6.91 s
[## ] | 6% Completed | 7.01 s
[### ] | 7% Completed | 7.11 s
[### ] | 7% Completed | 7.21 s
[### ] | 7% Completed | 7.31 s
[### ] | 7% Completed | 7.41 s
[### ] | 7% Completed | 7.51 s
[### ] | 7% Completed | 7.61 s
[### ] | 8% Completed | 7.71 s
[#### ] | 10% Completed | 7.81 s
[#### ] | 10% Completed | 7.91 s
[#### ] | 10% Completed | 8.01 s
[#### ] | 10% Completed | 8.11 s
[#### ] | 10% Completed | 8.21 s
[#### ] | 10% Completed | 8.31 s
[#### ] | 10% Completed | 8.42 s
[#### ] | 10% Completed | 8.52 s
[#### ] | 10% Completed | 8.62 s
[#### ] | 10% Completed | 8.72 s
[#### ] | 10% Completed | 8.82 s
[#### ] | 10% Completed | 8.92 s
[#### ] | 10% Completed | 9.02 s
[#### ] | 10% Completed | 9.12 s
[#### ] | 10% Completed | 9.22 s
[#### ] | 10% Completed | 9.32 s
[#### ] | 10% Completed | 9.42 s
[#### ] | 10% Completed | 9.52 s
[#### ] | 10% Completed | 9.62 s
[#### ] | 10% Completed | 9.72 s
[#### ] | 10% Completed | 9.82 s
[#### ] | 10% Completed | 9.92 s
[#### ] | 10% Completed | 10.02 s
[#### ] | 10% Completed | 10.12 s
[#### ] | 10% Completed | 10.22 s
[#### ] | 11% Completed | 10.32 s
[#### ] | 11% Completed | 10.42 s
[##### ] | 12% Completed | 10.52 s
[##### ] | 12% Completed | 10.62 s
[##### ] | 12% Completed | 10.72 s
[##### ] | 12% Completed | 10.82 s
[##### ] | 12% Completed | 10.92 s
[##### ] | 13% Completed | 11.02 s
[##### ] | 13% Completed | 11.12 s
[###### ] | 15% Completed | 11.22 s
[###### ] | 15% Completed | 11.32 s
[###### ] | 15% Completed | 11.42 s
[###### ] | 15% Completed | 11.52 s
[###### ] | 15% Completed | 11.62 s
[###### ] | 15% Completed | 11.72 s
[###### ] | 15% Completed | 11.82 s
[###### ] | 15% Completed | 11.92 s
[###### ] | 15% Completed | 12.02 s
[###### ] | 15% Completed | 12.12 s
[###### ] | 15% Completed | 12.22 s
[###### ] | 15% Completed | 12.32 s
[###### ] | 15% Completed | 12.42 s
[###### ] | 15% Completed | 12.52 s
[###### ] | 15% Completed | 12.62 s
[###### ] | 15% Completed | 12.72 s
[###### ] | 15% Completed | 12.82 s
[###### ] | 15% Completed | 12.92 s
[###### ] | 15% Completed | 13.02 s
[###### ] | 15% Completed | 13.12 s
[###### ] | 15% Completed | 13.22 s
[###### ] | 15% Completed | 13.32 s
[###### ] | 15% Completed | 13.42 s
[###### ] | 15% Completed | 13.52 s
[###### ] | 15% Completed | 13.62 s
[###### ] | 15% Completed | 13.72 s
[###### ] | 16% Completed | 13.82 s
[###### ] | 16% Completed | 13.92 s
[####### ] | 17% Completed | 14.02 s
[####### ] | 17% Completed | 14.13 s
[####### ] | 17% Completed | 14.23 s
[####### ] | 18% Completed | 14.33 s
[####### ] | 18% Completed | 14.43 s
[####### ] | 18% Completed | 14.53 s
[####### ] | 18% Completed | 14.63 s
[####### ] | 18% Completed | 14.73 s
[####### ] | 18% Completed | 14.83 s
[####### ] | 18% Completed | 14.93 s
[####### ] | 18% Completed | 15.03 s
[####### ] | 18% Completed | 15.13 s
[######## ] | 20% Completed | 15.23 s
[######## ] | 20% Completed | 15.33 s
[######## ] | 20% Completed | 15.43 s
[######## ] | 20% Completed | 15.53 s
[######## ] | 20% Completed | 15.63 s
[######## ] | 20% Completed | 15.73 s
[######## ] | 20% Completed | 15.83 s
[######## ] | 20% Completed | 15.93 s
[######## ] | 20% Completed | 16.03 s
[######## ] | 20% Completed | 16.13 s
[######## ] | 20% Completed | 16.23 s
[######## ] | 20% Completed | 16.33 s
[######## ] | 20% Completed | 16.43 s
[######## ] | 20% Completed | 16.53 s
[######## ] | 20% Completed | 16.63 s
[######## ] | 20% Completed | 16.73 s
[######## ] | 20% Completed | 16.83 s
[######## ] | 20% Completed | 16.93 s
[######## ] | 20% Completed | 17.03 s
[######## ] | 20% Completed | 17.13 s
[######## ] | 21% Completed | 17.23 s
[######## ] | 21% Completed | 17.33 s
[######### ] | 22% Completed | 17.43 s
[######### ] | 23% Completed | 17.53 s
[######### ] | 23% Completed | 17.63 s
[######### ] | 23% Completed | 17.73 s
[######### ] | 23% Completed | 17.83 s
[######### ] | 23% Completed | 17.93 s
[######### ] | 23% Completed | 18.03 s
[######### ] | 23% Completed | 18.13 s
[######### ] | 23% Completed | 18.23 s
[######### ] | 23% Completed | 18.33 s
[######### ] | 23% Completed | 18.43 s
[######### ] | 23% Completed | 18.53 s
[######### ] | 23% Completed | 18.63 s
[########## ] | 25% Completed | 18.73 s
[########## ] | 25% Completed | 18.83 s
[########## ] | 25% Completed | 18.93 s
[########## ] | 25% Completed | 19.03 s
[########## ] | 25% Completed | 19.13 s
[########## ] | 25% Completed | 19.23 s
[########## ] | 25% Completed | 19.33 s
[########## ] | 25% Completed | 19.43 s
[########## ] | 25% Completed | 19.54 s
[########## ] | 25% Completed | 19.64 s
[########## ] | 25% Completed | 19.74 s
[########## ] | 25% Completed | 19.84 s
[########## ] | 25% Completed | 19.94 s
[########## ] | 25% Completed | 20.04 s
[########## ] | 25% Completed | 20.14 s
[########## ] | 25% Completed | 20.24 s
[########## ] | 25% Completed | 20.34 s
[########## ] | 25% Completed | 20.44 s
[########## ] | 26% Completed | 20.54 s
[########## ] | 26% Completed | 20.64 s
[########## ] | 26% Completed | 20.74 s
[########## ] | 26% Completed | 20.84 s
[########## ] | 26% Completed | 20.94 s
[########### ] | 27% Completed | 21.04 s
[########### ] | 28% Completed | 21.14 s
[########### ] | 28% Completed | 21.24 s
[########### ] | 28% Completed | 21.34 s
[########### ] | 28% Completed | 21.44 s
[########### ] | 28% Completed | 21.54 s
[########### ] | 28% Completed | 21.64 s
[########### ] | 28% Completed | 21.74 s
[########### ] | 28% Completed | 21.84 s
[########### ] | 28% Completed | 21.94 s
[########### ] | 28% Completed | 22.04 s
[########### ] | 28% Completed | 22.14 s
[########### ] | 28% Completed | 22.24 s
[############ ] | 30% Completed | 22.34 s
[############ ] | 30% Completed | 22.44 s
[############ ] | 30% Completed | 22.54 s
[############ ] | 30% Completed | 22.64 s
[############ ] | 30% Completed | 22.74 s
[############ ] | 30% Completed | 22.84 s
[############ ] | 30% Completed | 22.94 s
[############ ] | 30% Completed | 23.04 s
[############ ] | 30% Completed | 23.14 s
[############ ] | 30% Completed | 23.24 s
[############ ] | 30% Completed | 23.34 s
[############ ] | 30% Completed | 23.44 s
[############ ] | 30% Completed | 23.54 s
[############ ] | 30% Completed | 23.64 s
[############ ] | 30% Completed | 23.74 s
[############ ] | 30% Completed | 23.84 s
[############ ] | 30% Completed | 23.94 s
[############ ] | 30% Completed | 24.04 s
[############ ] | 31% Completed | 24.14 s
[############ ] | 31% Completed | 24.24 s
[############ ] | 31% Completed | 24.34 s
[############# ] | 32% Completed | 24.44 s
[############# ] | 33% Completed | 24.54 s
[############# ] | 33% Completed | 24.64 s
[############# ] | 33% Completed | 24.74 s
[############# ] | 33% Completed | 24.85 s
[############# ] | 33% Completed | 24.95 s
[############# ] | 33% Completed | 25.05 s
[############# ] | 33% Completed | 25.15 s
[############# ] | 33% Completed | 25.25 s
[############# ] | 33% Completed | 25.35 s
[############# ] | 33% Completed | 25.45 s
[############# ] | 33% Completed | 25.55 s
[############# ] | 33% Completed | 25.65 s
[############# ] | 33% Completed | 25.75 s
[############# ] | 33% Completed | 25.85 s
[############# ] | 33% Completed | 25.95 s
[############# ] | 33% Completed | 26.05 s
[############# ] | 33% Completed | 26.15 s
[############# ] | 33% Completed | 26.25 s
[############# ] | 33% Completed | 26.35 s
[############# ] | 33% Completed | 26.45 s
[############## ] | 35% Completed | 26.55 s
[############## ] | 35% Completed | 26.65 s
[############## ] | 35% Completed | 26.75 s
[############## ] | 35% Completed | 26.85 s
[############## ] | 35% Completed | 26.95 s
[############## ] | 35% Completed | 27.05 s
[############## ] | 35% Completed | 27.15 s
[############## ] | 36% Completed | 27.25 s
[############## ] | 36% Completed | 27.35 s
[############## ] | 36% Completed | 27.45 s
[############## ] | 36% Completed | 27.55 s
[############## ] | 36% Completed | 27.65 s
[############## ] | 36% Completed | 27.75 s
[############## ] | 36% Completed | 27.85 s
[############## ] | 36% Completed | 27.95 s
[############## ] | 36% Completed | 28.05 s
[############## ] | 36% Completed | 28.15 s
[############### ] | 37% Completed | 28.25 s
[############### ] | 37% Completed | 28.35 s
[############### ] | 37% Completed | 28.45 s
[############### ] | 37% Completed | 28.55 s
[############### ] | 37% Completed | 28.65 s
[############### ] | 38% Completed | 28.75 s
[############### ] | 38% Completed | 28.85 s
[############### ] | 38% Completed | 28.95 s
[############### ] | 38% Completed | 29.05 s
[############### ] | 38% Completed | 29.15 s
[############### ] | 38% Completed | 29.25 s
[############### ] | 38% Completed | 29.35 s
[############### ] | 38% Completed | 29.45 s
[############### ] | 38% Completed | 29.55 s
[################ ] | 40% Completed | 29.65 s
[################ ] | 40% Completed | 29.75 s
[################ ] | 40% Completed | 29.85 s
[################ ] | 40% Completed | 29.95 s
[################ ] | 40% Completed | 30.05 s
[################ ] | 40% Completed | 30.16 s
[################ ] | 40% Completed | 30.26 s
[################ ] | 40% Completed | 30.36 s
[################ ] | 40% Completed | 30.46 s
[################ ] | 40% Completed | 30.56 s
[################ ] | 40% Completed | 30.66 s
[################ ] | 40% Completed | 30.76 s
[################ ] | 41% Completed | 30.86 s
[################ ] | 41% Completed | 30.96 s
[################ ] | 41% Completed | 31.06 s
[################ ] | 41% Completed | 31.16 s
[################ ] | 41% Completed | 31.26 s
[################ ] | 41% Completed | 31.36 s
[################ ] | 41% Completed | 31.46 s
[################ ] | 41% Completed | 31.56 s
[################ ] | 41% Completed | 31.66 s
[################ ] | 41% Completed | 31.76 s
[################# ] | 42% Completed | 31.86 s
[################# ] | 42% Completed | 31.96 s
[################# ] | 42% Completed | 32.06 s
[################# ] | 43% Completed | 32.16 s
[################# ] | 43% Completed | 32.26 s
[################# ] | 43% Completed | 32.36 s
[################# ] | 43% Completed | 32.46 s
[################# ] | 43% Completed | 32.56 s
[################# ] | 43% Completed | 32.66 s
[################# ] | 43% Completed | 32.76 s
[################# ] | 43% Completed | 32.86 s
[################# ] | 43% Completed | 32.96 s
[################# ] | 43% Completed | 33.06 s
[################# ] | 43% Completed | 33.16 s
[################# ] | 43% Completed | 33.26 s
[################# ] | 43% Completed | 33.36 s
[################# ] | 43% Completed | 33.46 s
[################# ] | 43% Completed | 33.56 s
[################# ] | 43% Completed | 33.66 s
[################# ] | 43% Completed | 33.76 s
[################## ] | 45% Completed | 33.86 s
[################## ] | 45% Completed | 33.96 s
[################## ] | 45% Completed | 34.06 s
[################## ] | 46% Completed | 34.16 s
[################## ] | 46% Completed | 34.26 s
[################## ] | 46% Completed | 34.36 s
[################## ] | 46% Completed | 34.46 s
[################## ] | 46% Completed | 34.56 s
[################## ] | 46% Completed | 34.66 s
[################## ] | 46% Completed | 34.76 s
[################## ] | 46% Completed | 34.86 s
[################## ] | 46% Completed | 34.96 s
[################## ] | 46% Completed | 35.06 s
[################## ] | 46% Completed | 35.16 s
[################## ] | 46% Completed | 35.26 s
[################## ] | 46% Completed | 35.36 s
[################## ] | 46% Completed | 35.46 s
[################## ] | 46% Completed | 35.57 s
[################### ] | 47% Completed | 35.67 s
[################### ] | 47% Completed | 35.77 s
[################### ] | 48% Completed | 35.87 s
[################### ] | 48% Completed | 35.97 s
[################### ] | 48% Completed | 36.07 s
[################### ] | 48% Completed | 36.17 s
[################### ] | 48% Completed | 36.27 s
[################### ] | 48% Completed | 36.37 s
[################### ] | 48% Completed | 36.47 s
[################### ] | 48% Completed | 36.57 s
[################### ] | 48% Completed | 36.67 s
[################### ] | 48% Completed | 36.77 s
[################### ] | 48% Completed | 36.87 s
[################### ] | 48% Completed | 36.97 s
[################### ] | 48% Completed | 37.07 s
[################### ] | 48% Completed | 37.17 s
[################### ] | 48% Completed | 37.27 s
[################### ] | 48% Completed | 37.37 s
[#################### ] | 50% Completed | 37.47 s
[#################### ] | 50% Completed | 37.57 s
[#################### ] | 51% Completed | 37.67 s
[#################### ] | 51% Completed | 37.77 s
[#################### ] | 51% Completed | 37.87 s
[#################### ] | 51% Completed | 37.97 s
[#################### ] | 51% Completed | 38.07 s
[#################### ] | 51% Completed | 38.17 s
[#################### ] | 51% Completed | 38.27 s
[#################### ] | 51% Completed | 38.37 s
[#################### ] | 51% Completed | 38.47 s
[#################### ] | 51% Completed | 38.57 s
[#################### ] | 51% Completed | 38.67 s
[#################### ] | 51% Completed | 38.77 s
[#################### ] | 51% Completed | 38.87 s
[#################### ] | 51% Completed | 38.97 s
[#################### ] | 51% Completed | 39.07 s
[##################### ] | 52% Completed | 39.17 s
[##################### ] | 52% Completed | 39.27 s
[##################### ] | 53% Completed | 39.37 s
[##################### ] | 53% Completed | 39.47 s
[##################### ] | 53% Completed | 39.57 s
[##################### ] | 53% Completed | 39.67 s
[##################### ] | 53% Completed | 39.77 s
[##################### ] | 53% Completed | 39.87 s
[##################### ] | 53% Completed | 39.97 s
[##################### ] | 53% Completed | 40.07 s
[##################### ] | 53% Completed | 40.17 s
[##################### ] | 53% Completed | 40.27 s
[##################### ] | 53% Completed | 40.37 s
[##################### ] | 53% Completed | 40.47 s
[##################### ] | 53% Completed | 40.57 s
[##################### ] | 53% Completed | 40.67 s
[##################### ] | 53% Completed | 40.77 s
[##################### ] | 53% Completed | 40.87 s
[##################### ] | 53% Completed | 40.97 s
[##################### ] | 53% Completed | 41.07 s
[##################### ] | 53% Completed | 41.18 s
[##################### ] | 53% Completed | 41.28 s
[###################### ] | 55% Completed | 41.38 s
[###################### ] | 55% Completed | 41.48 s
[###################### ] | 55% Completed | 41.58 s
[###################### ] | 55% Completed | 41.68 s
[###################### ] | 55% Completed | 41.78 s
[###################### ] | 55% Completed | 41.88 s
[###################### ] | 55% Completed | 41.98 s
[###################### ] | 56% Completed | 42.08 s
[####################### ] | 57% Completed | 42.18 s
[####################### ] | 58% Completed | 42.28 s
[####################### ] | 58% Completed | 42.38 s
[####################### ] | 58% Completed | 42.48 s
[####################### ] | 58% Completed | 42.58 s
[####################### ] | 58% Completed | 42.68 s
[####################### ] | 58% Completed | 42.78 s
[####################### ] | 58% Completed | 42.88 s
[####################### ] | 58% Completed | 42.98 s
[####################### ] | 58% Completed | 43.08 s
[####################### ] | 58% Completed | 43.18 s
[####################### ] | 58% Completed | 43.28 s
[####################### ] | 58% Completed | 43.38 s
[####################### ] | 58% Completed | 43.48 s
[####################### ] | 58% Completed | 43.58 s
[####################### ] | 58% Completed | 43.68 s
[####################### ] | 58% Completed | 43.78 s
[####################### ] | 58% Completed | 43.88 s
[####################### ] | 58% Completed | 43.98 s
[####################### ] | 58% Completed | 44.08 s
[####################### ] | 58% Completed | 44.18 s
[####################### ] | 58% Completed | 44.28 s
[######################## ] | 60% Completed | 44.38 s
[######################## ] | 60% Completed | 44.48 s
[######################## ] | 60% Completed | 44.58 s
[######################## ] | 60% Completed | 44.68 s
[######################## ] | 60% Completed | 44.78 s
[######################## ] | 60% Completed | 44.88 s
[######################## ] | 60% Completed | 44.98 s
[######################## ] | 61% Completed | 45.08 s
[######################## ] | 61% Completed | 45.18 s
[######################## ] | 61% Completed | 45.28 s
[######################## ] | 61% Completed | 45.38 s
[######################## ] | 61% Completed | 45.48 s
[######################### ] | 62% Completed | 45.58 s
[######################### ] | 62% Completed | 45.68 s
[######################### ] | 62% Completed | 45.78 s
[######################### ] | 62% Completed | 45.89 s
[######################### ] | 63% Completed | 45.99 s
[######################### ] | 63% Completed | 46.09 s
[######################### ] | 63% Completed | 46.19 s
[######################### ] | 63% Completed | 46.29 s
[######################### ] | 63% Completed | 46.39 s
[######################### ] | 63% Completed | 46.49 s
[######################### ] | 63% Completed | 46.59 s
[######################### ] | 63% Completed | 46.69 s
[######################### ] | 63% Completed | 46.79 s
[######################### ] | 63% Completed | 46.89 s
[######################### ] | 63% Completed | 46.99 s
[######################### ] | 63% Completed | 47.09 s
[######################### ] | 63% Completed | 47.19 s
[######################### ] | 63% Completed | 47.29 s
[######################### ] | 63% Completed | 47.39 s
[######################### ] | 63% Completed | 47.49 s
[######################### ] | 63% Completed | 47.59 s
[######################### ] | 63% Completed | 47.69 s
[########################## ] | 65% Completed | 47.79 s
[########################## ] | 65% Completed | 47.89 s
[########################## ] | 66% Completed | 47.99 s
[########################## ] | 66% Completed | 48.09 s
[########################## ] | 66% Completed | 48.19 s
[########################### ] | 67% Completed | 48.29 s
[########################### ] | 67% Completed | 48.39 s
[########################### ] | 67% Completed | 48.49 s
[########################### ] | 67% Completed | 48.59 s
[########################### ] | 67% Completed | 48.69 s
[########################### ] | 67% Completed | 48.79 s
[########################### ] | 67% Completed | 48.89 s
[########################### ] | 68% Completed | 48.99 s
[########################### ] | 68% Completed | 49.09 s
[########################### ] | 68% Completed | 49.19 s
[########################### ] | 68% Completed | 49.29 s
[########################### ] | 68% Completed | 49.39 s
[########################### ] | 68% Completed | 49.49 s
[########################### ] | 68% Completed | 49.59 s
[########################### ] | 68% Completed | 49.69 s
[########################### ] | 68% Completed | 49.79 s
[########################### ] | 68% Completed | 49.89 s
[########################### ] | 68% Completed | 49.99 s
[########################### ] | 68% Completed | 50.09 s
[########################### ] | 68% Completed | 50.19 s
[########################### ] | 68% Completed | 50.29 s
[########################### ] | 68% Completed | 50.39 s
[########################### ] | 68% Completed | 50.49 s
[############################ ] | 70% Completed | 50.59 s
[############################ ] | 70% Completed | 50.69 s
[############################ ] | 70% Completed | 50.79 s
[############################ ] | 70% Completed | 50.89 s
[############################ ] | 70% Completed | 50.99 s
[############################ ] | 71% Completed | 51.09 s
[############################ ] | 71% Completed | 51.19 s
[############################ ] | 71% Completed | 51.30 s
[############################ ] | 71% Completed | 51.40 s
[############################ ] | 71% Completed | 51.50 s
[############################# ] | 72% Completed | 51.60 s
[############################# ] | 72% Completed | 51.70 s
[############################# ] | 72% Completed | 51.80 s
[############################# ] | 72% Completed | 51.90 s
[############################# ] | 72% Completed | 52.00 s
[############################# ] | 72% Completed | 52.10 s
[############################# ] | 73% Completed | 52.20 s
[############################# ] | 73% Completed | 52.30 s
[############################# ] | 73% Completed | 52.40 s
[############################# ] | 73% Completed | 52.50 s
[############################# ] | 73% Completed | 52.60 s
[############################# ] | 73% Completed | 52.70 s
[############################# ] | 73% Completed | 52.80 s
[############################# ] | 73% Completed | 52.90 s
[############################# ] | 73% Completed | 53.00 s
[############################# ] | 73% Completed | 53.10 s
[############################# ] | 73% Completed | 53.20 s
[############################# ] | 73% Completed | 53.30 s
[############################# ] | 73% Completed | 53.40 s
[############################# ] | 73% Completed | 53.50 s
[############################# ] | 73% Completed | 53.60 s
[############################# ] | 73% Completed | 53.70 s
[############################## ] | 75% Completed | 53.80 s
[############################## ] | 75% Completed | 53.90 s
[############################## ] | 75% Completed | 54.00 s
[############################## ] | 75% Completed | 54.10 s
[############################## ] | 75% Completed | 54.20 s
[############################## ] | 75% Completed | 54.30 s
[############################## ] | 75% Completed | 54.40 s
[############################## ] | 75% Completed | 54.50 s
[############################## ] | 75% Completed | 54.60 s
[############################## ] | 76% Completed | 54.70 s
[############################## ] | 76% Completed | 54.80 s
[############################## ] | 76% Completed | 54.90 s
[############################## ] | 76% Completed | 55.00 s
[############################## ] | 76% Completed | 55.10 s
[############################## ] | 76% Completed | 55.20 s
[############################## ] | 76% Completed | 55.30 s
[############################## ] | 76% Completed | 55.40 s
[############################## ] | 76% Completed | 55.50 s
[############################## ] | 76% Completed | 55.60 s
[############################## ] | 76% Completed | 55.70 s
[############################## ] | 76% Completed | 55.80 s
[############################## ] | 76% Completed | 55.90 s
[############################### ] | 78% Completed | 56.00 s
[############################### ] | 78% Completed | 56.10 s
[############################### ] | 78% Completed | 56.20 s
[############################### ] | 78% Completed | 56.30 s
[############################### ] | 78% Completed | 56.40 s
[############################### ] | 78% Completed | 56.50 s
[############################### ] | 78% Completed | 56.60 s
[############################### ] | 78% Completed | 56.71 s
[############################### ] | 78% Completed | 56.81 s
[############################### ] | 78% Completed | 56.91 s
[############################### ] | 78% Completed | 57.01 s
[############################### ] | 78% Completed | 57.11 s
[############################### ] | 78% Completed | 57.21 s
[############################### ] | 78% Completed | 57.31 s
[################################ ] | 80% Completed | 57.41 s
[################################ ] | 80% Completed | 57.51 s
[################################ ] | 80% Completed | 57.61 s
[################################ ] | 80% Completed | 57.71 s
[################################ ] | 80% Completed | 57.81 s
[################################ ] | 80% Completed | 57.91 s
[################################ ] | 80% Completed | 58.01 s
[################################ ] | 80% Completed | 58.11 s
[################################ ] | 80% Completed | 58.21 s
[################################ ] | 80% Completed | 58.31 s
[################################ ] | 80% Completed | 58.41 s
[################################ ] | 80% Completed | 58.51 s
[################################ ] | 80% Completed | 58.61 s
[################################ ] | 80% Completed | 58.71 s
[################################ ] | 80% Completed | 58.81 s
[################################ ] | 80% Completed | 58.91 s
[################################ ] | 80% Completed | 59.01 s
[################################ ] | 80% Completed | 59.11 s
[################################ ] | 81% Completed | 59.21 s
[################################ ] | 81% Completed | 59.31 s
[################################# ] | 82% Completed | 59.41 s
[################################# ] | 82% Completed | 59.51 s
[################################# ] | 82% Completed | 59.61 s
[################################# ] | 83% Completed | 59.71 s
[################################# ] | 83% Completed | 59.81 s
[################################# ] | 83% Completed | 59.91 s
[################################# ] | 83% Completed | 60.01 s
[################################# ] | 83% Completed | 60.11 s
[################################# ] | 83% Completed | 60.21 s
[################################# ] | 83% Completed | 60.31 s
[################################# ] | 83% Completed | 60.41 s
[################################# ] | 83% Completed | 60.51 s
[################################# ] | 83% Completed | 60.61 s
[################################# ] | 83% Completed | 60.71 s
[################################## ] | 85% Completed | 60.81 s
[################################## ] | 85% Completed | 60.91 s
[################################## ] | 85% Completed | 61.01 s
[################################## ] | 85% Completed | 61.11 s
[################################## ] | 85% Completed | 61.21 s
[################################## ] | 85% Completed | 61.31 s
[################################## ] | 85% Completed | 61.41 s
[################################## ] | 85% Completed | 61.51 s
[################################## ] | 85% Completed | 61.62 s
[################################## ] | 85% Completed | 61.72 s
[################################## ] | 85% Completed | 61.82 s
[################################## ] | 85% Completed | 61.92 s
[################################## ] | 85% Completed | 62.02 s
[################################## ] | 85% Completed | 62.12 s
[################################## ] | 85% Completed | 62.22 s
[################################## ] | 85% Completed | 62.32 s
[################################## ] | 85% Completed | 62.42 s
[################################## ] | 86% Completed | 62.52 s
[################################## ] | 86% Completed | 62.62 s
[################################## ] | 86% Completed | 62.72 s
[################################## ] | 86% Completed | 62.82 s
[################################## ] | 86% Completed | 62.92 s
[################################## ] | 86% Completed | 63.02 s
[################################## ] | 86% Completed | 63.12 s
[################################### ] | 87% Completed | 63.22 s
[################################### ] | 87% Completed | 63.32 s
[################################### ] | 88% Completed | 63.42 s
[################################### ] | 88% Completed | 63.52 s
[################################### ] | 88% Completed | 63.62 s
[################################### ] | 88% Completed | 63.72 s
[################################### ] | 88% Completed | 63.82 s
[################################### ] | 88% Completed | 63.92 s
[################################### ] | 88% Completed | 64.02 s
[################################### ] | 88% Completed | 64.12 s
[################################### ] | 88% Completed | 64.22 s
[################################### ] | 88% Completed | 64.32 s
[################################### ] | 88% Completed | 64.42 s
[################################### ] | 88% Completed | 64.52 s
[################################### ] | 88% Completed | 64.62 s
[################################### ] | 88% Completed | 64.72 s
[################################### ] | 88% Completed | 64.82 s
[################################### ] | 88% Completed | 64.92 s
[################################### ] | 88% Completed | 65.02 s
[################################### ] | 88% Completed | 65.12 s
[################################### ] | 88% Completed | 65.22 s
[################################### ] | 88% Completed | 65.32 s
[#################################### ] | 90% Completed | 65.42 s
[#################################### ] | 90% Completed | 65.52 s
[#################################### ] | 90% Completed | 65.62 s
[#################################### ] | 90% Completed | 65.72 s
[#################################### ] | 90% Completed | 65.82 s
[#################################### ] | 90% Completed | 65.92 s
[#################################### ] | 90% Completed | 66.02 s
[#################################### ] | 90% Completed | 66.12 s
[#################################### ] | 90% Completed | 66.22 s
[#################################### ] | 90% Completed | 66.32 s
[#################################### ] | 91% Completed | 66.42 s
[#################################### ] | 91% Completed | 66.52 s
[#################################### ] | 91% Completed | 66.62 s
[#################################### ] | 91% Completed | 66.72 s
[#################################### ] | 91% Completed | 66.82 s
[#################################### ] | 91% Completed | 66.93 s
[#################################### ] | 91% Completed | 67.03 s
[#################################### ] | 91% Completed | 67.13 s
[#################################### ] | 91% Completed | 67.23 s
[#################################### ] | 91% Completed | 67.33 s
[##################################### ] | 92% Completed | 67.43 s
[##################################### ] | 92% Completed | 67.53 s
[##################################### ] | 92% Completed | 67.63 s
[##################################### ] | 92% Completed | 67.73 s
[##################################### ] | 92% Completed | 67.83 s
[##################################### ] | 92% Completed | 67.93 s
[##################################### ] | 92% Completed | 68.03 s
[##################################### ] | 93% Completed | 68.13 s
[##################################### ] | 93% Completed | 68.23 s
[##################################### ] | 93% Completed | 68.33 s
[##################################### ] | 93% Completed | 68.43 s
[##################################### ] | 93% Completed | 68.53 s
[##################################### ] | 93% Completed | 68.63 s
[##################################### ] | 93% Completed | 68.73 s
[##################################### ] | 93% Completed | 68.83 s
[##################################### ] | 93% Completed | 68.93 s
[##################################### ] | 93% Completed | 69.03 s
[##################################### ] | 93% Completed | 69.13 s
[###################################### ] | 95% Completed | 69.23 s
[###################################### ] | 95% Completed | 69.33 s
[###################################### ] | 95% Completed | 69.43 s
[###################################### ] | 95% Completed | 69.53 s
[###################################### ] | 95% Completed | 69.63 s
[###################################### ] | 95% Completed | 69.73 s
[###################################### ] | 95% Completed | 69.83 s
[###################################### ] | 95% Completed | 69.93 s
[###################################### ] | 95% Completed | 70.03 s
[###################################### ] | 95% Completed | 70.13 s
[###################################### ] | 95% Completed | 70.23 s
[###################################### ] | 95% Completed | 70.33 s
[###################################### ] | 95% Completed | 70.43 s
[###################################### ] | 95% Completed | 70.53 s
[###################################### ] | 95% Completed | 70.63 s
[###################################### ] | 95% Completed | 70.73 s
[###################################### ] | 95% Completed | 70.83 s
[###################################### ] | 96% Completed | 70.93 s
[###################################### ] | 96% Completed | 71.03 s
[###################################### ] | 96% Completed | 71.13 s
[###################################### ] | 96% Completed | 71.23 s
[###################################### ] | 96% Completed | 71.33 s
[###################################### ] | 96% Completed | 71.43 s
[####################################### ] | 97% Completed | 71.53 s
[####################################### ] | 97% Completed | 71.63 s
[####################################### ] | 97% Completed | 71.73 s
[####################################### ] | 97% Completed | 71.83 s
[####################################### ] | 98% Completed | 71.93 s
[####################################### ] | 98% Completed | 72.03 s
[####################################### ] | 98% Completed | 72.13 s
[####################################### ] | 98% Completed | 72.23 s
[####################################### ] | 98% Completed | 72.33 s
[####################################### ] | 98% Completed | 72.43 s
[####################################### ] | 98% Completed | 72.53 s
[####################################### ] | 98% Completed | 72.64 s
[####################################### ] | 98% Completed | 72.74 s
[####################################### ] | 98% Completed | 72.84 s
[########################################] | 100% Completed | 72.94 s
Plot RGB image time series
datacube[["red", "green", "blue"]].ed.plot_rgb(
col="time", col_wrap=4, vmax=0.2
)

<xarray.plot.facetgrid.FacetGrid object at 0x7f71f8a91190>
Plot mean RGB time series
datacube[["blue", "green", "red", "nir"]].groupby("time").mean(...).to_array(
dim="band"
).plot(col="band")
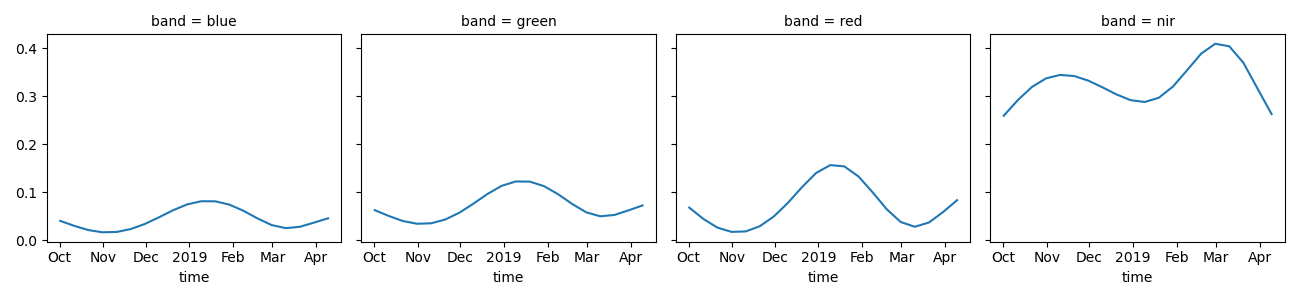
<xarray.plot.facetgrid.FacetGrid object at 0x7f71fc3277d0>
Plot NDVI evolution
datacube["ndvi"] = (datacube["nir"] - datacube["red"]) / (
datacube["nir"] + datacube["red"]
)
fig, ax = plt.subplots()
mean_ndvi = datacube[["ndvi"]].groupby("time").mean(...).to_array(dim="band")
std_ndvi = datacube[["ndvi"]].groupby("time").std(...).to_array(dim="band")
ax.fill_between(
mean_ndvi.time,
(mean_ndvi.values + std_ndvi.values)[0, ...],
(mean_ndvi.values - std_ndvi.values)[0, ...],
alpha=0.3,
color="C1",
)
mean_ndvi.plot(ax=ax, c="C1")
plt.grid(alpha=0.4)
plt.title("NDVI evolution every 10 days")
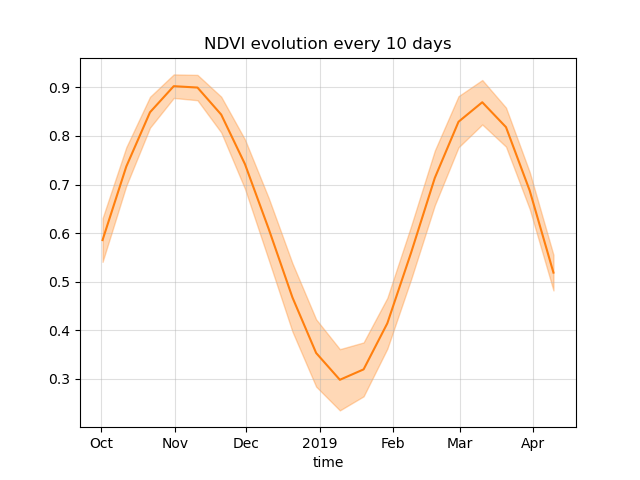
Text(0.5, 1.0, 'NDVI evolution every 10 days')
Total running time of the script: (1 minutes 31.998 seconds)